Los Polinomios
Clases de Polinomios:
Los polinomios se clasifican de acuerdo al número de términos. Un polinomio que tiene un solo término se llama monomio. Si el polinomio tiene dos términos se llama un binomio y si tiene tres términos se llama trinomio. Los polinomios formados por más de tres términos no reciben ningún nombre en especial, simplemente son polinomios con la cantidad de términos que contiene.
Ejemplos:
Monomios
|
Binomios
|
Trinomios
|
3x
|
7x - 4
|
n2 + 3n + 2
|
25
|
3a + 5b
|
3x4 – x3 + 5x2
|
-9x2y3
|
n2 – 3n
|
4xy + 9xy2 – 11xy4
|
El polinomio 8x3 + 5x2 - 3x + 7 es un polinomio de cuatro términos. *
"A partir de este momento trabajaremos ya sólo con polinomios con una sola letra (x) por considerar que son los más utilizados en la práctica " Ejemplo 9.- Para calcular la suma de los polinomios: (4x4 - 2x3 + 3x2 - 2x + 5 ) + ( 5x3 - x2 + 2x ) Basta sumar los términos de grados 3, 2 y 1 de ambos polinomios y dejar el resto de los términos del primero como está. Podemos indicar la suma de la siguiente forma para verla mejor: Por tanto: Para sumar dos o más polinomios se suman los términos semejantes de cada uno de ellos.4x4 - 2x3 + 3x2 - 2x + 5 Si en lugar de sumar dos polinomios se tratara de restarlos, bastaría cambiar el signo a todos los términos del segundo y sumar los resultados. Ejemplo 10.- Para calcular la diferencia o resta de los dos polinomios anteriores: (4x4 - 2x3 + 3x2 - 2x + 5 ) - ( 5x3 - x2 + 2x ) Se calcula la suma: (4x4 - 2x3 + 3x2 - 2x + 5 ) + ( - 5x3 + x2 - 2x ) = 4x4 - 7x3 + 4x2 - 4x + 5 La escena siguiente presenta la suma y la resta de dos polinomios de grado máximo 3, siendo posible cambiar los coeficientes de cada uno de ellos. Téngase en cuenta que si un coeficiente es 0, el término correspondiente vale 0, luego no suma ni resta y viceversa, si "falta" un término podemos suponer que el coeficiente es 0. | ||
| Ejercicio 6.- Calcula en tu cuaderno de trabajo la suma y la resta de los dos siguientes polinomios.a) ( - x3 + 5x2 - x + 1 ) + ( 5x2 - x - 3 ) b) ( 6x2 - x + 4 ) + ( 5x3 - x - 1) La suma del caso a) es la que se presenta en la escena adjunta. Cambia después los valores de los coeficientes (se llaman c1 a c4 para el primer polinomio y c5 a c8 para el segundo) de la escena para realizar la resta del caso y la suma y resta del caso b). | ||
Si uno de los dos polinomios es un monomio, la operación es simple como se puede ver en la escena siguiente, en la que se pueden variar los coeficientes.
En el caso en que ambos polinomios consten de varios términos, se puede indicar la multiplicación de forma semejante a como se hace con número de varias cifras, cuidando de situar debajo de cada monomio los que sean semejantes.
En la siguiente imagen se puede ver el producto de dos polinomios de varios términos.
Ejemplo 11.-
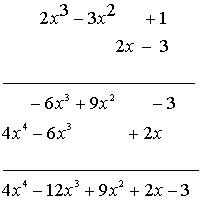
En la práctica no suele indicarse la multiplicación como en esta imagen, sino que suelen colocarse todos los términos seguidos y sumar después los que sean semejantes. Así:
Ejemplo 12.- ( - 2x3 + 3x2 - 2x + 5 ) · (x + 1) = (-2x4 +3x3 -2x2 + 5x - 2x3 + 3x2 - 2x + 5) = - 2x4 + x3+ x2 +3x + 5.
Las más usuales son: Cuadrado de un binomio: suma (a + b)2 o diferencia (a - b)2 Naturalmente realizar un cuadrado es multiplicar el binomio por sí mismo, luego: (a + b)2 = (a + b ) · (a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2 " El cuadrado de una suma es igual al cuadrado del primero más dos veces el primero por el segundo más el cuadrado del segundo " De modo similar: (a - b)2 = a2 - 2ab + b2 ( igual que antes pero cambiando el signo central). "En cualquier caso se debe tener en cuenta que el primer término "a" también puede ser negativo y por tanto cambiar el signo central". "En general se puede considerar siempre como una suma y para cada término asignarle el signo que le preceda (ver ejemplo 13 - b) Ejemplo 13.- a) (2x + 3y)2 = (2x)2 + 2 · 2x · 3y + (3y)2 = 4x2 +12xy + 9y2 b) (- x + 3)2 = (-x)2 + 2 · (-x) · 3 + 32 = x2 - 6x + 9 Suma por diferencia: se refiere al producto de la suma de dos monomios por la diferencia de ellos mismos: (a + b) · (a - b) = a2 - ab + ba + b2 = a2 - b2 Siempre recordamos que " suma por diferencia es igual a la diferencia de los cuadrados" . Otras igualdades importantes pero menos utilizadas pueden son: Cubo de una suma: (a + b)3 = a3 + 3a2b + 3ab2 +b3 Cuadrado de un trinomio: (a + b + c)2 = a2+ b2 +c2 + 2ab+ 2ac + 2bc
| |||||||||||||
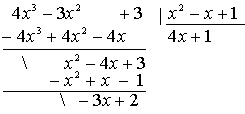
Los polinomios y sus aplicaciones son muy importantes en la ciencia e ingeniería. Los métodos numéricos requieren que los algoritmos proporcionen variedad de esquemas aplicados al modelo matemático del problema.
ResponderEliminarTambién son importantes en la informática, en los formateos que utilizan códigos e incognitas, por eso los informáticos utilizan los polinomios constantemente.
Bueno, los polinomios están muy ligados al álgebra. Resolver ecuaciones algebraicas, por ejemplo, es equivalente a hallar los ceros o raíces de un polinomio. Es por ello que aprender a factorizar y completar cuadrados, te permitiría no sólo hallar los valores de x que anulan a un polinomio, sino también resolver ecuaciones algebraicas.
ResponderEliminarCuando enseñan polinomios, normalmente enseñan que para sumar o restar dos términos éstos deben ser semejantes; que la multiplicación de polinomios se hace a través de la propiedad distributiva; que algunas multiplicaciones (o productos) son notables; que es posible convertir algunos polinomios en productos de dos o más factores (factorización); que la división de polinomios permite simplificar expresiones y que todo esto permite manipular fracciones algebraicas. El objetivo es claro: enseñar a manipular expresiones algebraicas, conocimiento que es fundamental para cualquier curso de álgebra y cálculo.
En su clasificación están los polinomios especiales y son los siguientes:
ResponderEliminar1) Polinomio completo: Podemos decir que un polinomio es completo con respecto a una letra cuando contiene todos los exponentes consecutivos de una letra, desde el más alto, al más bajo.Ejemplo:6x3 -5x + 3x5 +x2 -x4 +5
2) Polinomios Ordenados: Se le puede llamar polinomios ordenados cuando los exponentes van en orden. Se les llama polinomios ordenados ascendentes cuando los exponentes van subiendo y polinomios ordenados descendentes cuando los exponentes van bajando. Ejemplo: 5a2 +3a3 -a5 +a8
3) Polinomios homogéneos: Se les puede llamar polinomios homogéneos a los que el resultado de la suma de los exponentes de cada término es el mismo. Ejemplo: (3a2b + 5ab2 -3abc) Primer término: 3a2b1, sumados los exponentes 2 +1 =3, segundo término: +5a1b2, sumados los exponentes 1 +2 = 3, tercer término: -9a1b1c1, sumados los exponentes 1 +1 +1 = 3
4) Polinomio nulo: Es aquel polinomio en el que tiene todos sus coeficientes son iguales a cero; carece de grado.
5) Polinomio opuesto: Cuando los coeficientes de los términos de igual grado son números opuestos
Los polinomios sirven en el cálculo de la alineación de antenas electromagnéticas.
ResponderEliminarEjemplo: *El trabajo consiste en obtener una antena ranurada resonante para aplicarla a redes WiFi en la banda de 2.4 GHz. El diseño de la antena se hace empleando los polinomios de Chevyshev para determinar la distribución de corriente de cada elemento
del arreglo y con base en estos datos, encontrar las dimensiones físicas de dicha antena. Se han simulado diferentes condiciones para la antena, tales como: cambios en el nivel de lóbulo principal a secundario, diferente número de ranuras manteniendo fija la frecuencia de operación.
Como observamos en el blog, podemos decir que los polinomios aritméticos son todas expresiones matemáticas que combinan sumas y diferencias, el cual se hace por el uso de signos de agrupación que se emplean con el propósito de marcar cuales de las operaciones matemáticas deben ser efectuadas primero.
ResponderEliminarAquí podemos ver algo más sobre polinomios que son:
Operaciones con polinomios
Suma de polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3 Q(x) = 4x − 3x2 + 2x3
1Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3− 3x2 + 9x − 3
Resta de polinomios
La resta de polinomios consiste en sumar el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x− 4x − 3
P(x) − Q(x) = 3x2 + x − 3
http://www.ditutor.com/polinomios/polinomios.html
El algebra es quizá, la herramienta mas poderosa para llegar a la solución de problemas. Con el uso de constantes y variables se puede representar un sinnúmero de situaciones, se generalizan eventos y se da solución a casos particulares. A través del algebra se simplifican y se generaliza todo aquello relacionado con los números: operaciones y relaciones, junto con sus propiedades. Por eso los polinomios aparecen en los lugares más inesperados.
ResponderEliminarLos polinomios es muy amplia en los campos de:
-La ciencia, Ingeniería, Administración, Arquitectura, Matemática,Algebra.
También son importantes en:
- La informática
- En los formateos que utilizan códigos e incógnitas, por eso los informáticos utilizan los polinomios constantemente.