CONTADORES MATEMÀTICOS: abril 2013

martes, 23 de abril de 2013

Porcentajes(%)

Porcentajes

"Porcentaje quiere decir partes por 100"

Definición:En matemáticas, un porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador. También se le llama comúnmente tanto por ciento, donde por ciento significa “de cada cien unidades”. Se usa para definir relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, donde tanto es un número, se refiere a la parte proporcional a ese número de unidades de cada cien de esa cantidad. el porcentaje sirve también para sacar un por ciento de una cantidad.

Representación:

El tanto por ciento como fracción

El tanto por ciento se divide entre 100 y se simplifica la fracción. Ejemplo:

Para saber como se representa el 10 % en fracción se divide y luego se simplifica:

$10\,% = \cfrac{10}{100} = \cfrac{1}{10} = 0,1$

El porcentaje

La fracción común se multiplica por 100 y se resuelve la operación, como resultado será el porcentaje.

Ejemplo: Para representar 1/10 como un porcentaje se hace la operación siguiente:

$\cfrac{1}{10}= \cfrac{10}{100} = 10\,%$

Cuando dices "por ciento" en realidad dices "por cada 100"

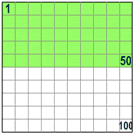	Así que 50% quiere decir 50 por 100 (50% de la caja es verde)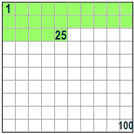
	Y 25% quiere decir 25 por 100 (25% de la caja es verde)

Ejemplos: Porcentajes de 80

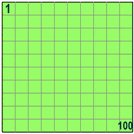	100% of 80 is ¹⁰⁰/₁₀₀ × 80 = 80 So 100% means all.
	50% of 80 is ⁵⁰/₁₀₀ × 80 = 40 So 50% means half.
	5% of 80 is ⁵/₁₀₀ × 80 = 4 So 5% means ⁵/_100ths.

Usando porcentajes

Como "por ciento" quiere decir "por cada 100" deberías pensar siempre que "hay que dividir por 100"

Así que 75% quiere decir ⁷⁵/₁₀₀

Y 100% es ¹⁰⁰/₁₀₀, o exactamente 1 (100% de cualquier número es el mismo número)

Y 200% es ²⁰⁰/₁₀₀, o exactamente 2 (200% de cualquier número es el doble del número)

Usa la barra de la izquierda y experimenta un poco (por ejemplo, ¿cuánto es el 60% de 80?)

Un porcentaje también se puede escribir como un decimal o una fracción

La mitad se puede escribir...

Como porcentaje:	50%
Como decimal:	0,5
Como fracción:	¹/₂

Algunos ejemplos detallados


Calcula 25% de 80
25% = ²⁵/₁₀₀		(²⁵/₁₀₀) × 80 = 20
Así que 25% de 80 es 20


Un Skateboard tiene una rebaja de 25%. El precio normal es $120. Calcula el nuevo precio
Calcula 25% de $120
25% = ²⁵/₁₀₀		(²⁵/₁₀₀) × $120 = $30
25% de $120 es $30
Así que la reducción es $30
Quita la reducción del precio original		$120 - $30 = $90
El precio del Skateboard en rebajas es $90

a) Aumentos porcentuales

Para incrementar una cantidad en un porcentaje, primero calculamos lo que representa el porcentaje de esa cantidad y luego se lo sumamos a dicha cantidad.

Ejemplo: incrementa 150 en un 20%.
Calculamos cuanto es un 20% de 150:
20% de 150 = (20 x 150) / 100 = 30
Este importe se lo sumamos al importe inicial:
150 + 30 = 180

Otro problema que se puede plantear es una cantidad varía de un importe inicial a un importe final y queremos saber en qué porcentaje se ha incrementado.

Por ejemplo, un automóvil que valía 12.000 euros ha incrementado su precio a 13.500 euros. ¿Qué porcentaje se ha incrementado?
Se calcula aplicando la fórmula:
% variación = (Importe final - Importe inicial) x 100 / Importe inicial
En el ejemplo:
% variación = (13.500 – 12.000) x 100 / 12.000 = 12,5%

b) Disminuciones porcentuales

Para disminuir una cantidad en un porcentaje, calculamos lo que representa el porcentaje de dicha cantidad y luego se lo restamos.

Ejemplo: disminuye 90 en un 40%.
Calculamos cuanto es un 40% de 90:
40% de 90 = (40 x 90) / 100 = 36
Este importe se lo restamos al importe inicial:
90 - 36 = 54

Al igual que en el caso anterior, se puede plantear el problema de unacantidad que disminuye de un importe inicial a un importe final y queremos saber en qué porcentaje lo ha hecho.

Por ejemplo, un televisor que valía 900 euros ahora cuesta 720 euros. ¿Qué porcentaje ha disminuido?
Se aplica la misma fórmula que en el punto anterior:
% variación = (Importe final - Importe inicial) x 100 / Importe inicial
En el ejemplo:
% variación = (720 – 900) x 100 / 900 = -20%

c) Repartos proporcionales

Tres amigos salen a pasear: el primero toma 3 helados, el segundo 2 helados y el tercero 1 helado. El total de la consumición es 36 euros ¿Cuánto tiene que pagar cada uno?
No podemos dividir el importe entre 3 porque cada uno de ellos ha tomado un número diferente de helados.
Para realizar un reparto proporcional, en función del número de helados tomados, aplicamos una regla de 3 simple:
Entre los 3 amigos han tomado 6 helados:
El primero de los amigos ha tomado 3:
6 helados ------> 36 euros
3 helados ------>“a” euros
Siendo “a” = (36 x 3) / 6 = 18 euros tiene que pagar el primer amigo
El segundo de los amigos ha tomado 2:
6 helados ------> 36 euros
2 helados ------>“b” euros
Siendo “b” = (36 x 3) / 6 = 12 euros euros tiene que pagar el segundo amigo
El tercero de los amigos tan sólo ha tomado 1:
6 helados ------> 36 euros
1 helados ------>“c” euros
Siendo “c” = (36 x 1) / 6 = 6 euros euros tiene que pagar el tercer amigo

Bibliografias:

INTEGRANTES:

·         Morelia Acosta Polo

·         Mardeli Alayo Nolasco

·         César Becerra Urbina

·         Yerson Moreno Carrasco

·         Stefanie Reyna Mendoza

·         Kevín Valdelomar Álvarez

·         Ivone Zavaleta Cabrera

martes, 16 de abril de 2013

CONJUNTOS

DEFINICIÓN

Llamaremos conjunto a toda colección de objetos y elemento a cada uno de los objetos de un conjunto. Un conjunto se puede definir de dos formas: por extensión (citando cada elemento) y por comprensión (citando una propiedad que verifican todos sus elementos).

REPRESENTACIÓN DE UN CONJUNTO

Por diagrama Entre llaves

S = {a, e, i, o, u}

Se escribe una coma para separar los

elementos.

OPERACIONES CON CONJUNTOS

· Unión: (símbolo ∪) La unión de dos conjuntos A y B, que se representa como A ∪ B), es el conjunto de todos los elementos que pertenecen al menos a uno de los conjuntos A y B.

· Intersección: (símbolo ∩) La intersección de dos conjuntos A y B es el conjunto A ∩ B de los elementos comunes a A y B.

· Diferencia: (símbolo \) La diferencia del conjunto A con B es el conjunto A \ B que resulta de eliminar de A cualquier elemento que esté en B.

· Complemento: El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos que no pertenecen a A, respecto a un conjunto U que lo contiene.

· Diferencia simétrica: (símbolo Δ) La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.

TIPOS DE CONJUNTOS :

1) Conjuntos disjuntos: Son aquellos conjuntos que no tienen elementos en común.

Por ejemplo:

2) Conjunto Subconjunto: Un conjunto es subconjunto de otro si todos los elementos de un conjunto también pertenecen al otro.

Ejemplo:

APLICACIÓN DE CONJUNTOS:

1. 1. En las matemáticas: se utilizan conjuntos de objetos matemáticos tales como conjuntos de números, conjuntos de polinomios, conjuntos de puntos o de rectas, etc.; pero con el ﬁn de aclarar los conceptos al principiante, puede ser útil considerar en los ejemplos conjuntos integrados por objetos comunes en la vida diaria

2. 2. Los elementos de un conjunto pueden ser, a su vez, conjuntos de elementos de otros conjuntos. Por ejemplo, mediante un proceso elemental de abstracción, podemos pensar que una biblioteca es un conjunto de libros, que un libro es el conjunto de sus páginas, que una página de un libro es el conjunto de sus líneas de texto, etc.

3. 3. En la vida diaria se pueden formar todo tipo de conjuntos, por ejemplo: Cuando vas a ordenar tu ropa tienes que separarlos en distintas prendas como en un cajón van los pantalones, en otro vas los polos y así todo tipo de prendas y entre todo eso de forman varios conjuntos de prendas.

4. 4. Otro ejemplo de conjuntos pueden ser los tipos de música, hay de diferentes tipos como rock, pop, etc. y así también se pueden formar conjuntos de tipos de música y agruparlos de diferente manera y escuchar lo que te guste y elegir el tipo que más te guste.

5. 5. En los animales también estaríamos empleando los conocimientos del conjunto para clasificarlos en aves, mamíferos, reptiles, batracios, insectos.
Acá los están clasificando de acuerdo a sus características formando conjuntos de aves, mamíferos, entre otros antes dichos.

BIBLIOGRAFÍAS :

http://www.profesorenlinea.cl/quinto/matematica/ConjuntosTiposde.htm

http://www4.ujaen.es/~magarcia/algebra1inf_archivos/Tema2ap.pdf

http://personales.unican.es/ruizvc/algebra/conjuntos1.pdf

http://es.wikipedia.org/wiki/Conjunto#Operaciones_con_conjuntos

INTEGRANTES:

· Morelia Acosta Polo

· Mardeli Alayo Nolasco

· César Becerra Urbina

· Yerson Moreno Carrasco

· Stefanie Reyna Mendoza

· Kevín Valdelomar Álvarez

· Ivone Zavaleta Cabrera

martes, 9 de abril de 2013

LA HISTORIA DE LOS NUMEROS

Historia de los números

HISTORIA DE LOS NÚMEROS NATURALES

Antes de que surgieran los números para la representación de cantidades, el ser humano usó otros métodos para contar, utilizando para ello objetos como piedras, palitos de madera, nudos de cuerdas, o simplemente los dedos. Más adelante comenzaron a aparecer los símbolos gráficos como señales para contar, por ejemplo marcas en una vara o simplemente trazos específicos sobre la arena. Pero fue en Mesopotamia alrededor del año 4.000 a. C. donde aparecen los primeros vestigios de los números que consistieron en grabados de señales en formas de cuñas sobre pequeños tableros de arcilla empleando para ello un palito aguzado. De aquí el nombre de escritura cuneiforme. Este sistema de numeración fue adoptado más tarde, aunque con símbolos gráficos diferentes, en la Grecia Antigua y en la Antigua Roma. En la Grecia antigua se empleaban simplemente las letras de sualfabeto, mientras que en la antigua Roma además de las letras, se utilizaron algunos símbolos.

Quien colocó al conjunto de los números naturales sobre lo que comenzaba a ser una base sólida, fue Richard Dedekind en elsiglo XIX. Que después precisó Peano dentro de una lógica de segundo orden, resultando así los famosos cinco postulados que llevan su nombre. Frege fue superior a ambos, demostrando la existencia del sistema de números naturales partiendo de principios más fuertes. Lamentablemente la teoría de Frege perdió, por así decirlo, su credibilidad y hubo que buscar un nuevo método. FueZermelo quien demostró la existencia del conjunto de números naturales, dentro de su teoría de conjuntos y principalmente mediante el uso del axioma de infinitud que, con una modificación de este hecha por Adolf Fraenkel, permite construir el conjunto de números naturales como ordinales según von Neumann

HISTORIA DE LOS NUMEROS ENTEROS

El hombre desde principios de la evolución siempre utilizó recursos para facilitar su relación con el medio que lo rodea. Es consecuencia de ese proceso la redacción de este artículo.

En las siguientes líneas daremos una breve y sustancial descripción acerca de los números enteros en la historia.

Desde la era primitiva el hombre siempre buscó respuestas a sus inquietudes. La inquietud permitió la aparición de conceptos abstractos en la mente del hombre primitivo ya evolucionado. Cuando el hombre desarrolla la capacidad de darle sentido racional a las cosas, nace el concepto de cantidad.

Inicialmente no utilizábamos la notación indo – arábiga, sino representábamos, las cantidades, con marcas en los árboles, con un montón de piedras, nudos en sogas, etc. Los recursos que utilizábamos dependían de la cultura donde estábamos ubicados.

Diversas culturas representan la noción de cantidad según su desarrollo lo permitía. Fruto de esta diversidad nacen las notaciones de cantidad como la romana, babilónica, griega, etc. Se sabe que los babilonios utilizaron simples enteros positivos para tratar de contar unas pocas ovejas, mientras que hoy en día los enteros positivos no satisfacen el complejo mundo de las matemáticas. Desde luego el significado que cada grupo social asigna a un determinado conocimiento o idea, implica mucho en su visión de vida. Por ejemplo los pitagóricos tenían una explicación de la realidad basada en los números. Filolao, filósofo pitagórico, resume perfectamente el papel tan importante que se le otorgaba:

“El número reside en todo lo que es conocido. Sin él es imposible pensar nada ni conocer nada.”

Historia de los números racionales

Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.

Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.

En el siglo XIII, Leonardo de Pisa, llamado Fibonacci, famoso, entre otras cosas por la serie de Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.

A principios del siglo XV, el árabe Al Kashi fue el que generalizó el uso de los números decimales tal y como los conocemos hoy.

A finales del siglo XVI, Simon Stevin desarrolló y divulgó las fracciones decimales que se expresaban por medio de números decimales: décimas, centésimas, milésimas, etc., pero los escribía de una forma complicada; así para 456, 765 escribía 456 (0) 7(1) 6(2) 5(3).

A principios del siglo XVII, los números decimales ya aparecieron tal y como los escribimos hoy, separando con un punto o una coma la parte entera de la parte decimal. Los números decimales se impusieron, en casi todos los países, al adoptarse el Sistema Métrico Decimal, en el siglo XVIII, concretamente en 1792.

BREVE HISTORIA DE LOS NÚMEROS REALES

El concepto de número real se originó cuando se constató la existencia de los números irracionales. Así, el conjunto de los números reales se origina como la unión del conjunto de losnúmeros racionales y el conjunto de los irracionales.
Debido a que el conjunto de números reales contiene al conjunto de números racionales, y éste a su vez contiene a los enteros que a su vez contiene los números naturales, se sigue que el conjunto de los números reales contiene también a los números enteros y a los números naturales. Asimismo, el conjunto de números reales contiene al de los números irracionales.
Por tanto, los números reales pueden ser racionales o irracionales, algebraicos o trascendentes; y positivos,negativos, o cero.

Puede definirse un número real, en estos términos, como un número positivo o negativo que puede o no tener cifras de decimal finito o infinito y puede representarse mediante un punto en la recta de números reales. En este sentido, el teorema fundamental de la geometría analítica establece que a cada número real le corresponde un punto en la recta de los números reales y recíprocamente

Historia de los Números Complejos

Muchos conceptos en matemáticas tardaron varios años y hasta siglos en desarrollarse, desde el momento en que fueron descubiertos por primera vez, hasta la formalización de los mismos. El avance en el tiempo de la matemática fue un proceso lento, debido al carácter formal de esta ciencia: una de sus reglas es que cualquier objeto nuevo debe estar claramente definido para ser aceptado por toda la comunidad. Muchas ideas incompletas quedaron relegadas a la oscuridad y el olvido por no encajar en el sistema de razonamiento de la época, como fue el caso de los números complejos.

En Italia, durante el periodo del renacimiento, por vez primera los Algebristas se dedican a investigar seriamente estos números y penetran el cerco misterioso en que se hallaban envueltos desde la antigüedad. Los complejos aparecen inicialmente en el libro Ars magna de Girolamo Cardano, publicado en 1545.

Los números complejos fueron ignorados sistemáticamente, por su carácter extraño, carentes de sentido e imposibles de representar. Aparecen entre las soluciones de las ecuaciones cuadráticas, que generan raíces cuadradas de números negativos.

Por ejemplo la ecuación: x2 + x + 5 = 0

UN VIDEO SOBRE LA HISTORIA DEL 1