Porcentajes  "Porcentaje quiere decir partes por 100" Definición:En matemáticas, un porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador. También se le llama comúnmente tanto por ciento, donde por ciento significa “de cada cien unidades”. Se usa para definir relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, donde tanto es un número, se refiere a la parte proporcional a ese número de unidades de cada cien de esa cantidad. el porcentaje sirve también para sacar un por ciento de una cantidad. Representación:El tanto por ciento como fracción |
El tanto por ciento se divide entre 100 y se simplifica la fracción. Ejemplo:
Para saber como se representa el 10 % en fracción se divide y luego se simplifica:

El porcentaje
La fracción común se multiplica por 100 y se resuelve la operación, como resultado será el porcentaje.Ejemplo: Para representar 1/10 como un porcentaje se hace la operación siguiente:
Cuando dices "por ciento" en realidad dices "por cada 100"
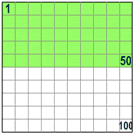 | Así que 50% quiere decir 50 por 100 (50% de la caja es verde) | 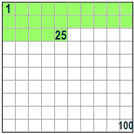 |
| Y 25% quiere decir 25 por 100 (25% de la caja es verde) |
Ejemplos: Porcentajes de 80
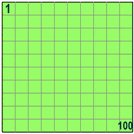 | 100% of 80 is 100/100 × 80 = 80
So 100% means all.
|
 |
50% of 80 is 50/100 × 80 = 40
So 50% means half.
|
 |
5% of 80 is 5/100 × 80 = 4
So 5% means 5/100ths.
|
Usando porcentajes
Como "por ciento" quiere decir "por cada 100" deberías pensar siempre que "hay que dividir por 100"
Así que 75% quiere decir 75/100
Y 100% es 100/100, o exactamente 1 (100% de cualquier número es el mismo número)
Y 200% es 200/100, o exactamente 2 (200% de cualquier número es el doble del número)
Usa la barra de la izquierda y experimenta un poco (por ejemplo, ¿cuánto es el 60% de 80?)
|
Un porcentaje también se puede escribir como un decimal o una fracción
 |
| ||||||||||
Algunos ejemplos detallados
Calcula 25% de 80 | ||
| 25% = 25/100 | (25/100) × 80 = 20 | |
Así que 25% de 80 es 20 | ||
Un Skateboard tiene una rebaja de 25%. El precio normal es $120. Calcula el nuevo precio | ||
Calcula 25% de $120 | ||
| 25% = 25/100 | (25/100) × $120 = $30 | |
25% de $120 es $30 | ||
Así que la reducción es $30 | ||
| Quita la reducción del precio original | $120 - $30 = $90 | |
El precio del Skateboard en rebajas es $90 | ||
a) Aumentos porcentuales
Para incrementar una cantidad en un porcentaje, primero calculamos lo que representa el porcentaje de esa cantidad y luego se lo sumamos a dicha cantidad.
Ejemplo: incrementa 150 en un 20%.
Calculamos cuanto es un 20% de 150:
20% de 150 = (20 x 150) / 100 = 30
Este importe se lo sumamos al importe inicial:
150 + 30 = 180
Otro problema que se puede plantear es una cantidad varía de un importe inicial a un importe final y queremos saber en qué porcentaje se ha incrementado.
Por ejemplo, un automóvil que valía 12.000 euros ha incrementado su precio a 13.500 euros. ¿Qué porcentaje se ha incrementado?
Se calcula aplicando la fórmula:
% variación = (Importe final - Importe inicial) x 100 / Importe inicial
En el ejemplo:
% variación = (13.500 – 12.000) x 100 / 12.000 = 12,5%
b) Disminuciones porcentuales
Para disminuir una cantidad en un porcentaje, calculamos lo que representa el porcentaje de dicha cantidad y luego se lo restamos.
Ejemplo: disminuye 90 en un 40%.
Calculamos cuanto es un 40% de 90:
40% de 90 = (40 x 90) / 100 = 36
Este importe se lo restamos al importe inicial:
90 - 36 = 54
Al igual que en el caso anterior, se puede plantear el problema de unacantidad que disminuye de un importe inicial a un importe final y queremos saber en qué porcentaje lo ha hecho.
Por ejemplo, un televisor que valía 900 euros ahora cuesta 720 euros. ¿Qué porcentaje ha disminuido?
Se aplica la misma fórmula que en el punto anterior:
% variación = (Importe final - Importe inicial) x 100 / Importe inicial
En el ejemplo:
% variación = (720 – 900) x 100 / 900 = -20%
c) Repartos proporcionales
Tres amigos salen a pasear: el primero toma 3 helados, el segundo 2 helados y el tercero 1 helado. El total de la consumición es 36 euros ¿Cuánto tiene que pagar cada uno?
No podemos dividir el importe entre 3 porque cada uno de ellos ha tomado un número diferente de helados.
Para realizar un reparto proporcional, en función del número de helados tomados, aplicamos una regla de 3 simple:
Entre los 3 amigos han tomado 6 helados:
El primero de los amigos ha tomado 3:
6 helados ------> 36 euros
3 helados ------>“a” euros
Siendo “a” = (36 x 3) / 6 = 18 euros tiene que pagar el primer amigo
El segundo de los amigos ha tomado 2:
6 helados ------> 36 euros
2 helados ------>“b” euros
Siendo “b” = (36 x 3) / 6 = 12 euros euros tiene que pagar el segundo amigo
El tercero de los amigos tan sólo ha tomado 1:
6 helados ------> 36 euros
1 helados ------>“c” euros
Siendo “c” = (36 x 1) / 6 = 6 euros euros tiene que pagar el tercer amigo
Bibliografias:
- http://www.aulafacil.com/matematicas-segundo-eso/Curso/Lecc-38.htm
- http://www.disfrutalasmatematicas.com/numeros/porcentajes.html
- http://es.wikipedia.org/wiki/Porcentaje
INTEGRANTES:
- · Morelia Acosta Polo· Mardeli Alayo Nolasco· César Becerra Urbina· Yerson Moreno Carrasco· Stefanie Reyna Mendoza· Kevín Valdelomar Álvarez· Ivone Zavaleta Cabrera

Son aquellas aplicaciones matemáticas para comprender el concepto de porcentajes, son las actividades sobre fracciones y decimales, fracciones y porcentajes, tanto por ciento, frecuencia, probabilidad y porcentajes, etc, para asi poder llevar una buena relación en una cantidad especifica que nos den en las proporciones. pues también tenemos:
ResponderEliminarPara determinar el porcentaje de un número siguiendo los siguientes pasos:
.Multiplica el número por el porcentaje (ej. 87 * 68 = 5916)
.Divide el resultado por 100 (Mueve el punto decimal dos lugares hacia la izquierda) (ej. 5916/100=59.16)
Redondea a la precisión deseada (ej. 59.16 redondeado al número entero más próximo=59).
En matemáticas, un porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador.
ResponderEliminarEl porcentaje se denota utilizando el símbolo %, que matemáticamente equivale al factor 0,01 y que se debe escribir después del número al que se refiere, dejando un espacio de separación.1 Por ejemplo, "treinta y dos por ciento" se representa mediante 32 % y significa 'treinta y dos de cada cien
El vocablo porcentaje tiene su origen en el inglés percentage, un término que se utiliza para escribir los números bajo la apariencia de una fracción de cien. El símbolo de este concepto es el %, el cual se denomina “por ciento” y se traduce como “de cada cien”. Por ejemplo: Diez por ciento es un porcentaje que se escribe como 10% y que se entiende como diez de cada cien. Si se dice que el 10% de un grupo de treinta personas tiene el pelo de color rojo, la frase supone que tres de esas personas son pelirrojas.
ResponderEliminarEl origen del signo” % “parece estar en la abreviatura italiana c° (de cento). Con el paso del tiempo, la c se cerró y la subraya de la ° se convirtió en una barra. Finalmente, los dos círculos pasaron a ser ceros por influencia del número 100.
ResponderEliminarUn porcentaje es una forma de expresar una proporción o fracción como una fracción de denominador 100, es decir, como una cantidad de centésimas. Es decir, una expresión como "45%" ("45 por ciento") es lo mismo que la fracción 45/100.
ResponderEliminarlos porcentajes estan en nuestra vida diaria por ejemplo cuando nos dan un descuento de un producto dado ya estamos realizando los porcentajes
ResponderEliminarEl porcentaje se usa para comparar una fraccion ( que indica la relacion entre dos cantidades )
ResponderEliminarCon otras expresandolas mediantes porcentajes para usar 100 como denominador comun
Un ejemplo : si en un pais hay 500 000 enfermos de gripre de un total de 10 millones de personas
Y en. Otro hay 150 000 de un total de un millon de personas , resulta mas claro en que el primer pais hay un 5% de personas con gripe .mientras el segundo pais hay un 15 % .resultado hay una proporcion mayor del. Segundo pais ....
El tanto por ciento se divide entre 100 y se simplifica la fracción. Ejemplo:
ResponderEliminarPara saber como se representa el 10 % en fracción se divide y luego se simplifica:
Para obtener un tanto por ciento de un número simplemente se multiplica. Por ejemplo, el 25 % de 150 es . Una forma equivalente de tratar esta operación es considerar que se multiplica por la cifra y se divide por cien (pues 0,01 = 1/100).
ResponderEliminarAlternativamente, en un método muy habitual antaño, se construye una regla de tres simple directa. Así, para calcular el 25% de 150 se hace la regla de tres: simplemente se multiplica cruzado y divide por el que queda solo o en conjunción con el restado.
Gracias por los recursos! Me ayudan mucho en mis clases de primaria. Recientemente, también he descubierto el blog de cursosgratuitos.eu donde hay un montón de recursos de aprendizaje por ejemplo de idiomas.
ResponderEliminarUn saludo :)